Introduction

Data flow analysis uses data flow information to solve a particular data flow problem such as determining reachability, dependence, and so on. The algorithms used to obtain data flow information may vary in terms of accuracy and precision. To help quantify effectiveness, data flow algorithms may generally be categorized based on specific sensitivities. The first category, referred to as flow sensitivity is used to convey whether or not an algorithm takes into account the implied order of instructions. Path sensitivity is used to convey whether or not an algorithm considers predicates. Finally, algorithms may also be context-sensitive if they take into account a calling context to restrict analysis to realizable paths when considering interprocedural data flow information.

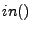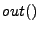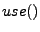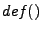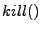Data flow information is typically collected by statically analyzing the data dependence of instructions or statements. For example, conventional def-use chains describe the variables that exist within $ in()$ , $ out()$ , $ use()$ , $ def()$ , and $ kill()$ set for each instruction or statement. Understanding data flow information with this level of detail makes it possible to statically solve a particular data flow problem. However, the resources needed to represent the def-use data flow information can be prohibitive when working with large applications. Depending on the data flow problem, the amount of data flow information required to come to a solution may be in excess of the physical resources present on a computer performing the analysis. This physical resource problem can be solved using at least two general approaches.

The most basic approach might involve simply partitioning, or fragmenting, analysis information such that smaller subsets are considered individually rather than attempting to represent the complete set of data flow information at once[15]. While this would effectively constrain the amount of physical resources required, it would also directly impact the accuracy and precision of the underlying algorithm used to perform data flow analysis. For instance, identifying the ``interesting portion'' of a program may require more state than can be feasibly obtained in single program fragment. A second and potentially more optimal approach might involve generalizing data flow information. By generalizing data flow information, an algorithm can operate within the bounds of physical resources by making use of a more abstract view of the complete set of data flow information. The distinction between the generalizing approach and the partitioning approach is that the generalized data flow information should not affect the accuracy of the algorithm since it should still be able to represent the complete set of generalized data flow information at once.

There has been significant prior work that has illustrated the effectiveness of generalizing data flow information when performing data flow analysis. The def-use information obtained between instructions or statements has been generalized to describe sets for basic blocks. Horwitz, Reps, and Binkley describe how a system dependence graph (SDG) can be derived from intraprocedural data flow information to produce a summary graph which convey context-sensitive data flow information at the procedure level[7]. Their paper went on to describe an interprocedural slicing algorithm that made use of SDGs. Reps, Horwitz, and Sagiv later described a general framework (IFDS) in which many data flow analysis problems can be solved as graph reachability problems[13,14]. The algorithms proposed in their paper focus on restricting analysis to interprocedurally realizable paths to improve precision. Identifying interprocedurally realizable paths has since been compared to the concept of context-free-language (CFL) reachability (CFL-reachability)[8]. These algorithms have helped to form the basis for techniques used in this paper to both generalize and analyze data flow information.

This paper approaches the generalization of data flow information by defining generalization tiers at which data flow information can be conveyed. A generalization tier is intended to show the data flow relationships between a set of conceptual software elements. Examples of software elements include an instruction, a basic block, a procedure, a data type, and so on. To define these relationships, data flow information is collected at the most specific generalization tier, such as the instruction tier, and then generalized to increasingly less-specific generalization tiers, such as the basic block, procedure, and data type tiers. Figure 1 provides a visual representation of some of the generalization tiers which may exist for data flow information collected from a program. The concentric rings are meant to illustrate containment.

**Figure 1:** Logical generalization tiers at which data flow information can be described. Elaborate from least-specific to most-specific and generalize from most-specific to least-specific.

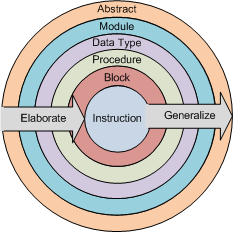To illustrate the usefulness of generalizing data flow information, this paper also presents a progressive algorithm that can be used to determine reachability between nodes on a data flow graph at each generalization tier. The algorithm starts by generating a data flow graph using data flow information from the least-specific generalization tier. The graph is then analyzed using a previously describe algorithm to determine reachability between an arbitrary set of nodes. The set of reachable paths found is then used to qualify the set of more-specific potentially reachable paths found at the next generalization tier. The more-specific paths are used to construct a new data flow graph. These steps then repeat using each more-specific generalization tier until it is not possible to obtained more detailed information. The benefit of this approach is that a minimal set of data flow information is considered as a result of progressively qualifying data flow paths at each generalization tier. It should be noted that different reachability problems may require state that is prohibitively large. As such, it is helpful to consider refining a reachability problem to operate more efficiently by making use of generalized information.

This paper is organized into two sections. §2 discusses the algorithms used to generalize data flow information at each generalization tier. §3 describes the algorithm used to determine reachable data flow paths by progressively analyzing data flow information at each generalization tier. It should be noted in advance that the author does not claim to be an expert in this field; rather, this paper is simply an explanation of the author's current thoughts. These thoughts attempt to take into account previous work whenever possible to the extent known by the author. Given that this is the case, the author is more than willing to receive criticism relating to the the ideas put forth in this paper.