

| Current | v9 | v8 | v7 | v6 | v5 | v4 | v3 | v2 | v1 | All | About |
BayesCompare Metric
BayesCompare was created as an attempt to use a well understood rule
to classify 802.11 implementations. In document classification, the
problem is that of given a set W of words appearing in a document,
classify the document as belonging to one of several categories. One
takes the category to be the category C that maximizes 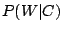
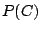 . The conditional probability
. The conditional probability 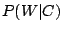 comes from a
training set of documents known to be in category C. If we take W
to be the set of durations occurring in a given packet capture that
we want to identify by implementation then
comes from a
training set of documents known to be in category C. If we take W
to be the set of durations occurring in a given packet capture that
we want to identify by implementation then 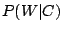 becomes the
probability of W occurring in a capture given that the capture comes
from 802.11 implementation C.
becomes the
probability of W occurring in a capture given that the capture comes
from 802.11 implementation C.
Classification in this manner is only as good as the training set
(print database). A given training set may not yet know that
implementation C can produce duration D. Hence 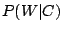 , which is
approximated from the training set, is zero when W contains D even
though W may contain another duration that uniquely identifies C.
Further, approximating
, which is
approximated from the training set, is zero when W contains D even
though W may contain another duration that uniquely identifies C.
Further, approximating 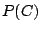 is problematic, as it is the
probability of seeing a given 802.11 implementation. One might
approximate it by perhaps chipset market share but this would be
somewhat inaccurate because it ignores the fact that a device driver
is part of an 802.11 implementation we wish to identify. Getting an
accurate approximation of it is difficult so we chose to ignore it.
This of course puts the metric at a slight disadvantage compared to
the other metrics, as we shall see.
is problematic, as it is the
probability of seeing a given 802.11 implementation. One might
approximate it by perhaps chipset market share but this would be
somewhat inaccurate because it ignores the fact that a device driver
is part of an 802.11 implementation we wish to identify. Getting an
accurate approximation of it is difficult so we chose to ignore it.
This of course puts the metric at a slight disadvantage compared to
the other metrics, as we shall see.
Let X be an 802.11 implementation for which a fingerprint exists in
the print database. Let L be the duration fingerprint arising from
an input pcap file. We want the probability that the input pcap file
originated with implementation X given L: 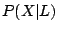 . Using Bayes
rule,
. Using Bayes
rule, 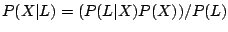 . The idea here is to use
these conditional probabilities to rank the degree of a match
between L and each fingerprint in the print database. Therefore, we
did not compute
. The idea here is to use
these conditional probabilities to rank the degree of a match
between L and each fingerprint in the print database. Therefore, we
did not compute 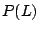 for a given input pcap as it is constant
across all fingerprints in the database. Of course probability P(X)
is not constant across all fingerprints but computing it is
problematic, as discussed above. Therefore, we didn't compute it as
part of the conditional probability. Further, to simplify things,
we approximated
for a given input pcap as it is constant
across all fingerprints in the database. Of course probability P(X)
is not constant across all fingerprints but computing it is
problematic, as discussed above. Therefore, we didn't compute it as
part of the conditional probability. Further, to simplify things,
we approximated 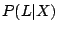 as the product
as the product 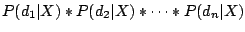 where
where 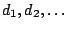 are the distinct
durations that appear in L. This assumes that the individual
duration values in L occur independently which one can argue isn't
true since the durations occur in sequence for certain control
frames, for instance, duration values in ACK, RTS and CTS frames.
But as mentioned previously, control frames are ignored in
fingerprints.
are the distinct
durations that appear in L. This assumes that the individual
duration values in L occur independently which one can argue isn't
true since the durations occur in sequence for certain control
frames, for instance, duration values in ACK, RTS and CTS frames.
But as mentioned previously, control frames are ignored in
fingerprints.
If L denotes the fingerprint arising from an input pcap file and R a
fingerprint in the print database then we take the preceding product
to be 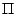 R.duration_ratio(d) where d ranges over all durations
in L. And when taking into account packet types in which durations
occur, it becomes
R.duration_ratio(d) where d ranges over all durations
in L. And when taking into account packet types in which durations
occur, it becomes 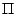 R.duration_ratio(p, d) where p and d range
over all packet types and durations respectively where duration d
occurs in a packet of type p in L.
R.duration_ratio(p, d) where p and d range
over all packet types and durations respectively where duration d
occurs in a packet of type p in L.
Figure 4.7:
BayesCompare duration value only analysis
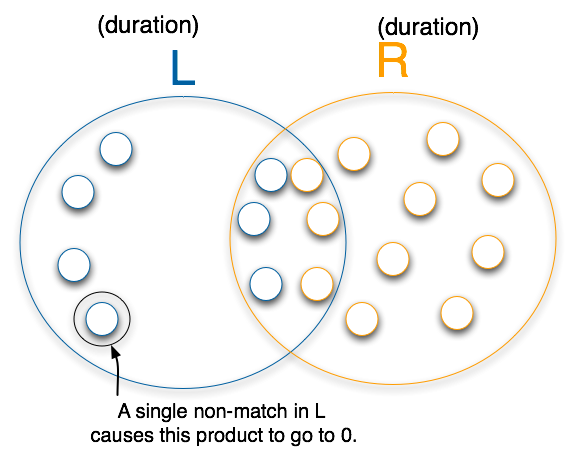
ret = 1.0 for every duration-value dret *= R.duration_ratio(d) return ret;
Figure 4.8:
BayesCompare (packet_type, duration) analysis
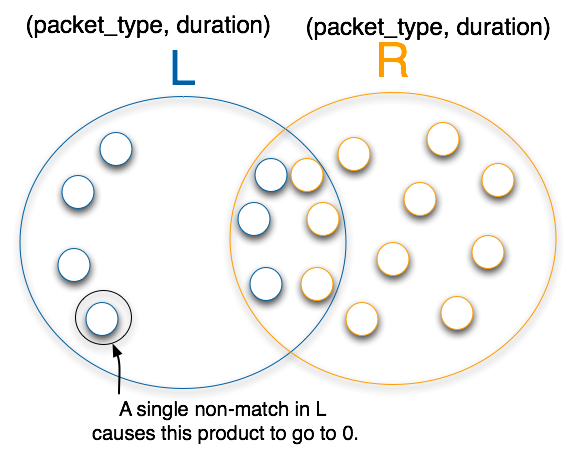
ret = 1.0 for every packet_type p, duration-value dret *= R.duration_ratio(p, d) return ret;